CCAI｜如何能既便宜又快速地獲取大數據？這位微軟研究員設計了兩個模型，幫你省錢省時間

美國微軟雷德蒙研究院首席研究員周登勇

文/CSDN賈維娣

7 月 22 - 23 日，在中國科學技術協會、中國科學院的指導下，由中國人工智能學會、阿裏巴巴集團 & 螞蟻金服主辦，CSDN、中國科學院自動化研究所承辦的 2017 中國人工智能大會（CCAI 2017）在杭州國際會議中心盛大召開。

大會第二天上午，美國微軟雷德蒙研究院首席研究員周登勇（Denny Zhou）發表了《眾包中的統計推斷與激勵機製》主題報告，從“為什麼眾包”、“眾包的挑戰”、“統計推斷”、“激勵機製”著手，結合多個生動形象的案例，具體總結了微軟雷德蒙研究院過去幾年在眾包研究與工程上的進展。

周登勇博士表示，在可以預見的將來，機器智能完全代替人的智能幾乎沒有任何可能，我們應該是讓人與機器各施所長互相補充。數據標注是一個比較簡單的人機係統，但這裏麵包含的技術已經相當有挑戰性。如果我們要建立更複雜的人機智能係統解決更大的問題，會有更多的新的困難需要克服。

以下為演講實錄，在不違背原意的情況下進行了刪減和調整。

大家好，我今天要講的是眾包。具體來說，我將討論如何通過眾包獲取高質量的數據標簽。為開發一個機器學習的智能係統，我們第一步要做的事情就是獲得高質量的帶標簽的數據。

為什麼需要眾包？

通過眾包我們很容易拿到大量的帶有標簽的數據。眾包有兩個優點：

速度快。一個商業眾包平台或許有上百萬甚至幾百萬的數據標記人員。

便宜。在亞馬遜眾包平台標注一個圖像數據通常都不到一美分。

所以，通過眾包很可以以很少的花費在短時間內獲得大量的帶標簽的數據。在機器學習裏大家經常會說的一句話：更多的數據會打敗一個聰明的算法。

如何提高眾包數據的質量

眾包存在的問題

可是，通過眾包獲取的數據標簽質量或許不高。 隻要原因如下：

專業技能。因為眾包人員可能沒有標記你的數據所需的技能。

動機。眾包人員沒有動力好好的把這個數據標記好。

如果使用低質量的數據去訓練一個機器學習模型，不管使用什麼高級的算法，都可能無濟於事。

眾包中的統計推斷

在一定程度上，統計推斷可以幫助我們從低質量的通過眾包獲得的數據標簽中提煉出正確的標簽。

讓我們先看一個假想的例子。比如這個橙子與橘子的分類問題。每幅圖像同時有幾個人標注，不同的人或給出不同的答案。但是，當把不同的答案設法結合起來，我們或許能知道正確的答案是什麼。這也通常叫做群體智慧。

怎麼結合不同人的答案呢？最簡單的辦法就是采用投票的方式。也就是說，哪一類標簽拿到的投票數是最多的，我們就認為這個圖像屬於這一類。

我們在做一個問題的時候，總應該想一想，我們的做法合理嗎？ 還有改進的空間嗎？ 在我我們的這個問題上， 投票意味著什麼呢？投票意味者所有人的水平都是一樣的。也就是說， 大家都一樣好。

顯然這在現實上不太可能。更可能的是大家的的水平參差不齊。但是，因為沒有正確的答案，我們不能立即知道誰的水平更高。而且，即使我們知道正確的標簽，也很難比較兩個人的水平的高低，因為不同的問題難度會很不一樣。一個答對了10道容易問題的人與答對10道難題的人水平或很不一樣。所以，為了推斷出正確的數據標簽，我們需要把把以上討論的關於人的水平與問題難度的直觀想法轉化成一個數學模型。

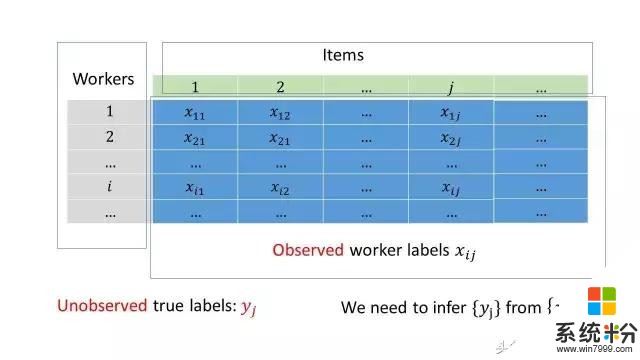
接下來講我們的方案。在這之前，讓我先引進一些數學符號。讓我們把收集來的眾包數據表示成一個矩陣這個矩陣的每一行對應一個數據標記員，每一列對應著我們需要標記的對象。數據表示第個人對第個數據做出的標記。真實的標簽是不知道的。我們需要解決的問題就是如何從推斷出。

極小極大熵原理

我們的解決方案叫極小極大熵原理，可以分成兩塊來解讀：

優化的對象；

優化的約束條件。

我們先看約束條件。第一個約束條件是針對每個數據標記員工，第二個約束條件是針對每個需要標記的對象。下麵我將解釋這兩個約束。我們會看到第一個約束條件對應著人的水平，第二個約束條件對應著問題的難度。

剛才說過，每一個數據標記人員所標記的數據對應著矩陣的一行。我們的約束做這麼一件簡單的事情：計數。我們數一下有多少類別為的對象被誤標為。約束方程的右邊是觀察到的誤標總數，左側則是對應的期望值。一個人誤標越多，水平就越低。

構造這個約束方程的原理可以理解如下。

假設我們有一枚硬幣，我們希望知道這個硬幣是正麵的概率是多大。假設我們把這個硬幣不斷的丟10次，有6次是正麵。那麼正麵的概率是多少呢？一般我們會說正麵的概率是60%。為什麼呢？我們可以這樣想。假設正麵的概率是p，我們會認定10 * p = 6，右邊是觀察到的正麵數，左邊是期望值。解這個方程，我們就可以得到p = 0.6。

類似的，我們對需要標記的每一個對象也有這樣的計數。當我們知道真實的類別的話，我們會知道有多少人標錯了。標錯的人越多，這個問題就越難。我們方程的右側統計一下到底有多少人標錯了，左邊則是是它的期望值。

約束條件已經講完了，現在回到為什麼采用這樣一種目標函數。首先我們把極小化放在一邊，先看極大化。也就是極大熵。我們用一個數學模型解釋觀察到的數據的時候，盡量用一個光滑的模型去擬合數據。類似地，當我們用一個概率分布解釋觀察到的數據的時候，會讓分布盡可能平坦。這就是極大熵原理的直觀解釋。為進一步推斷真實的標簽，我們極小化最大的熵。熵在直覺的意義上意味著不確定性。極小化最大的熵意味著極小化不確定性，也就是我們認為數據標記員都在盡力做好他們的工作。如果他們隻是提供隨機的標簽，那麼就沒有任何辦法去恢複真實的標簽。

解決極小極大的優化問題的時候，我們需要把它變成一個對偶問題，叫拉格朗日對偶。拉格朗日乘子與可以分別解釋成人的水平與問題的難度。我們初步設想是把每個人的能力與問題的難度給刻畫出來，但是並沒有假設這個模型是什麼樣的。當我們同時引進約束條件和極大極小化熵，這個模型就自動推出來了。要注意到這裏的拉格朗日乘子是矩陣，與ℓ是類別。非對角線上的元素（與ℓ不相等）表示怎麼把一個類別的標記對象，混淆成另外一個類別。對角線線上的數字 （與ℓ相等）則表示標記的精度。

我們現在討論以上模型的另外一種解釋方案，這個方式跟心理學有關。這是數學心理學家在60年代提出的想法，稱之為客觀性測量原理。比如說我們測量桌子長度的時候，假設一張桌子是另外一張的兩倍長。不管我們用什麼尺子去測量，這個永遠是另外一個的兩倍，這叫測量的客觀性。在眾包裏麵我們要做的測量是每個人的水平以及每個問題的難度。我們也要保證測量的方式足夠客觀。這意味著兩個人的水平的相對比較應該與用來測量人的水平的具體的問題是獨立的。把這個客觀性原理用數學刻劃出來的話，可以證明我們提出的眾包模型是唯一符合客觀性原理的模型。

我們的眾包模型很容易拓展到分級的數據上麵去。比如說我們在做搜索的時候，數據標簽通常是“完美”、“優秀”、“好“，“公平”，或者是“不好“。一個人可能把一個“完美”與“優秀”有混淆，但是不太可能把“完美“與”不好“混淆。當我們把這樣的直覺變成數學的描述，就構造了下麵的約束條件。

在第一個方程裏麵，我們檢查數據標記員的標簽是不是比某一個標簽c大，而且真實的是不是也比這個大，然後讓經驗觀察的次數與它的期望值相等。其他的方程可以類似解釋。

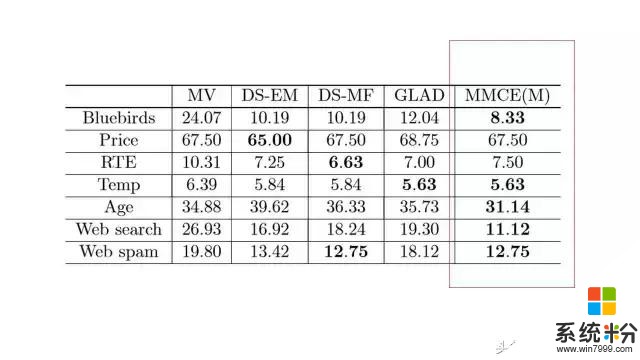
以上圖表是在眾包數據集上的實驗結果，每一個數字表示了錯誤率，我們方法的結果在最後一列。經驗結果表明我們的方法確實能產生比較好的性能，但是除了有一個數據集Price。在這個數據集裏麵，包含的是UCI本科學生對產品價格的估計。這個數據有係統性的偏差。學生們把價格普遍低估。這或許並不令人驚訝。

我們也考慮了預算最優的眾包問題。在這個問題裏麵，我們需要在每一步考慮兩個問題：哪一個數據需要更多的標記；以及讓誰來標注。在我們的方案裏麵，這個問題通過馬爾科夫決策理論解決。

眾包激勵措施

我要討論的下一個問題，就是在做眾包的時候怎麼付錢。我之所以想做這個問題，是因為我對前麵的解決方案並不是很滿意。盡管極小極大熵原理相對投票以及其他的方法準確率有很大的提高，但是我希望能有更大的提高。

如果我們想把一個問題的解決方案做出本質的提升，我們往往需要跳出原來的解決思路。我們注意到眾包遠不隻是機器學習的問題。眾包是個商業行為。眾包人員給我們標記數據的時候，我們需要付錢。如何付錢有可能是整個眾包數據質量的關鍵所在。

一個常用的付錢策略就是通過隨機抽查的答案的質量來決定付多少錢。具體操作起來，就是把一些我們已經知道答案的問題隨機分布在眾包任務裏麵（下圖裏麵紅方框表示已經知道標簽的圖像）。這些知道答案的問題通常稱為金色標準問題。數據標記人員不知道哪些問題是金色標準問題。我們根據一個數據標記人員在金色標準問題上的表現來決定付多少錢。

我們可以先想想怎麼付這個錢。比如說：

報酬正比於精度。假設我們有100個圖像需要標記，有4個圖像我們是知道答案的，但是數據標記員不知道哪4個圖案你是知道答案的，假設每個標記是兩分錢，有一個人答對了一個，正確率就是四分之一，報酬是4 x 2 x ¼ = 2。

超過一定精度才給錢。比如說精度超過了60%，我們就給錢，低於60%就不給錢。上麵那個例子裏麵就不給錢。

我們能否有更好的付錢方式呢？

允許跳過沒有把握的問題

付錢問題實際上有利益衝突在裏麵：數據標記人員希望用最小的努力拿到最大化的收益；雇主希望花最少的錢讓他們出最好的活。

一個好的付錢機製需要協調這個矛盾，達到雙贏。為解決這個問題我們需要用數學刻劃兩個概念，一個是“真實性“（truthful）準則，一個是”沒有免費的午餐“（no-free-lunch）準則。

“真實性”準則假設每個人在回答問題的時候會有一個信心（confidence）值，在0到1之間。如果他的信心值不到一定程度，他就不應該回答這個問題。反之，如果他的信心值足夠大，就應該回答這個問題。我們要設置一個付錢的機製，使得給你標記數據的人，能與你的想法互相配合。否則，這隻會是我們自己的一廂情願。

我舉一個例子解釋一下真實性準則。比如說我們讓人去標記一下這個狗是什麼種類。假設我們設定了一個信心值是50% （注意到隨機猜的正確率是1/3, 小於50%）。第一個人認為自己隻有30%的幾率認為會達到一個正確的答案。由於30% 小於給定的50%, 他就應該如實選擇“我不確定“。第二個人覺得自己有90%的幾率答案會是對的。 由於90% 大於50%，這種情況下她應該回答這個問題。

“沒有免費的午餐“準則決定在什麼情況不付錢: 如果一個雇員的所有沒有跳過去的問題的回答都是錯的，就不付錢。 這樣的雇員沒有給我們帶來任何價值。

現在的問題是我們要找到一個付錢的方式，同時滿足“真實性”和“沒有免費的午餐“，也就是說，使得雇員心甘情願做你想做的事情，而且沒做好的話就拿不到錢。一般來說，付錢的方式還不能太複雜，最好用簡單的加法和乘法就能解決。

這個是我們的付錢方式，一種乘法機製，或者叫做“翻倍或歸零”： 如果一個人犯了任何錯誤的話，就沒有錢了，否則的話拿到的收入采用乘積的方式往上增長。

歸零或讓人會覺得很殘酷。這裏需要解釋幾件事：

在做數據標記的時候，雇員可以跳過沒有把握的問題，他的收入不受影響。

眾包中我們往往會把巨大的數據標記任務分解成很多小任務。每個小任務幾分鍾之內就可以完成。如果沒有拿到錢的話，也是幾分鍾之內沒有拿到錢。一但沒有拿到錢，眾包人員知道自己做錯事情了，會從中吸取教訓，在下一輪裏麵做的更好。

我們可以給每個雇員固定的收入，隻是用這個方式計算額外收入或者獎金，就像你在公司工作的情況下，你的收入會分成好兩部分，基本工資與獎金。

讓我用例子解釋實際上如何使用這個付錢機製。在眾包之前需要很清楚地告訴雇員錢是怎麼付的。回到圖像標記這個問題上，我們或許給定這樣的付錢規則： 剛開始是一分錢，對每個正確的答案拿的錢就翻倍，如果有任何的答案是錯的情況下，錢就歸零了，如果跳過問題的話，不影響付錢。

比如第一個人前兩個答案是對的，收入等於1 x 2 x 2。後三個答案跳過去了。跳過去的時候收入不受影響（等價於乘1），所以總共拿到4分錢;

第二個人兩個答案是對的，兩個沒有回答，一個是錯的。在這個情況下收入是零，因為錯了一道題。

我們在亞馬遜眾包平台上做了實驗，發現使用這種付錢方式能夠把數據標注的錯誤率甚至可以降低60%。有沒有其他的付錢方式同時滿足“真實性”和“沒有免費的午餐“這兩個準則呢？令人驚奇的是，理論上可以證明，我們的付錢方式是唯一的可以滿足這兩個準則的付錢方式。 我們還有另外一個定理，假設有一個人所有的問題都跳過去，我們的付錢方式也是唯一的能夠給這些人付最少錢的方式。可能有人會好奇，為什麼這個人什麼問題都不回答也給錢？理論上我們證明了一個不可能性定理：如果一個人什麼問題都不回答就不給錢的話，那樣的付錢機製一定不能滿足“真實性”。

允許選擇一個子集（subset selection）

我們可以把剛才的方案做進一步的延伸。在許多情況下，雇員不知道真實的答案是什麼，但是知道哪些答案是錯的。比如這個狗的問題，他確信最後一個答案肯定是錯的，但是不肯定正確的答案到底是第一個還是第二個。於是，他就把前兩個答案都選上。這信息對我們來說是有用的，因為他排除了第三個答案。如果他把所有答案都選上了，相當於他沒有回答這個問題或者說把這個問題跳過去了。

在這種情況下，我們有一種類似的付錢方式。我們現在有一個表示子集的大小，全部答對的情況下拿到的總收入是 A，選擇的子集越大的話，拿到的錢越少。如果某這個選擇的子集沒有包含正確的答案，就不給錢。在這裏我們類似地定義“真實性”和“沒有免費的午餐“這兩個準則，並獲得類似的定理。

眾包數據標記的時候如果你沒有精力抽查，你可以再雇另外一批人幫你抽查結果，類似於每年你去開機器學習大會，你會發現大會主席不可能評價每篇論文該收還是不收，會雇傭一些論文審查人員審查論文。寫論文的作者在這裏相當於提供數據標簽的人，論文審查人員相當於這裏審查別人答案的人，大會主席就是你自己。在這種情況下我們也需要設計一個不同的付錢方式。

謝謝大家！